Hypothetical scenario: An engineer (or anyone who uses this code for that matter!) fits a response surface to some data on day 1. They repeat this exercise on day 2, where the data is moderately different. Can we identify sensitivities, moments, and subspaces on the difference between the two responses.
Rationale: The engineer wants to understand what changed between day 1 and day 2. Now the simplest solution would be to create another response surface on the difference between the two datasets. But what if the input samples where the same, the basis was the same, but only the output samples were different?
The above, and a few other musings, motivate this post.
Consider two polynomials $p_1$ and $p_2$. Our goal is to be able to carry out operations of the form
p1 = Poly()
p2 = Poly()
p3 = p1 - p2
where p3 is an instant of the Poly class. There are two important ideas to take note of here. First, any linear operation — whether integration, differentiation, addition, subtraction – on a polynomial will yield another polynomial, which makes this easy. Second, if the support of the two polynomials is different then we most certainly may not have a polynomial. Naturally, one can develop such methods in PolyTrees() more aptly, but for starters let’s consider the simplest scenario.
We add the following code to Poly()
def __add__(self, *args):
""" Adds polynomials.
Returns
-------
poly
An instance of the Poly class.
"""
polynew = deepcopy(self)
for other in args:
polynew.coefficients += other.coefficients
if np.all( polynew._quadrature_points - other._quadrature_points ) == 0:
polynew._model_evaluations += other._model_evaluations
return polynew
def __sub__(self, *args):
""" Subtracts polynomials.
Returns
-------
poly
An instance of the Poly class.
"""
polynew = deepcopy(self)
for other in args:
polynew.coefficients -= other.coefficients
if np.all( polynew._quadrature_points - other._quadrature_points ) == 0:
polynew._model_evaluations -= other._model_evaluations
return polynew
which permits us to do the following:
def fun_1(x):
return x**2 - 2*x + 3.2
def fun_2(x):
return x**2
def fun_3(x):
return -2*x + 10
p = Parameter(lower=-1., upper=1., order=2)
b = Basis('univariate')
# Poly 1
poly1 = Poly(p, b, method='numerical-integration')
poly1.set_model(fun_1)
# Poly 2
poly2 = Poly(p, b, method='numerical-integration')
poly2.set_model(fun_2)
# Poly 3
poly3 = Poly(p, b, method='numerical-integration')
poly3.set_model(fun_3)
# Test!
poly4 = poly1 + poly2
poly5 = poly1 - poly2 - poly3
# Plots!
poly4.plot_polyfit_1D(uncertainty=False)
poly5.plot_polyfit_1D(uncertainty=False)
Note that in practice, one can add or subtract as many polynomials as one desires!
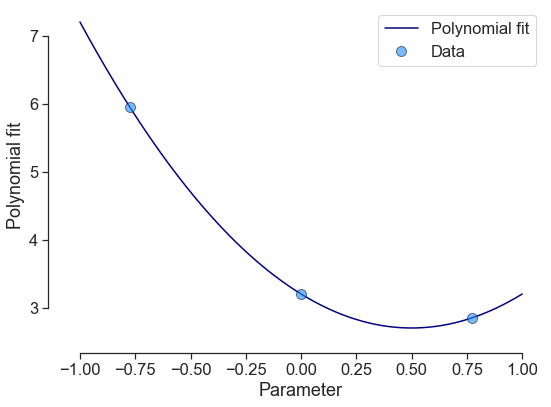
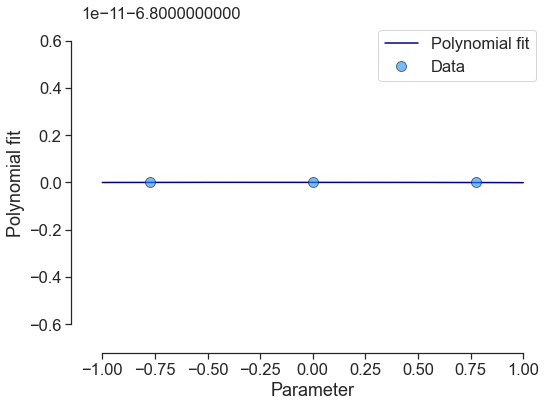
Code commit can be found below. The next step would be to:
- Have
__add__,__sub__, and__mul__operations on polynomials with different input sample locations. - Permit operations over different multi-index sets, provided the support for each parameter is the same.