Hello everyone, this is the third blog in the series of blogs I have written during the coding period of GSoC 2021. In the last blog, I explained the workflow of an under-construction Analytical Model. Within the time span of 2 weeks, we managed to make a lot of updates to the workflow, error-handling, styling of the layout and added better visualizations to gain meaningful insights from the underlying process. Not only this, we managed the deploy the web application on a server. Our application can be viewed at Link.
ADDITIONS TO THE ANALYTICAL MODEL
The newer version of the analytical model aims to improve the performance of the web application considering a better and dynamic user experience. The changes are as follows:
1.STYLE:
A much more dynamic approach has been taken to improve the parameter card. The size of theparameter card depends upon the number of parameters added. Changes to the style and spacing between input boxes have been made. Spacelab theme was used to modify the style of the application
Major changes were made to the Polynomial card. A dropdown list was added to access different order Sobol indices. Dynamic selection feature is added in the Sobol dropdown list and the solver method dropdown list. Taking an example of 1-dimensional Polynomial, for this Sobol indices would be disabled, subsequently, for a 2-dimensional Polynomial, Sobol indices of order 1 and order 2 are accessible.
2.WORKFLOW:
The workflow for uncertainty quantification is strict and the user needs to follow each step carefully to obtain the result. The workflow is updated to make it easier for the user to understand and use the app at its full potential. In the updated version the user can add parameters at any stage of the workflow and update the input function to compute uncertainty. Also, informative steps are provided in the application for users to understand the basic workflow.
3.Visualization:
The visualisations capability of the app is improved. The basis plot which had a single 2-D plot now consists of various options depending upon the number of parameters added. Following are the basis plots for 1-D,2-D and 3-D Polynomials.
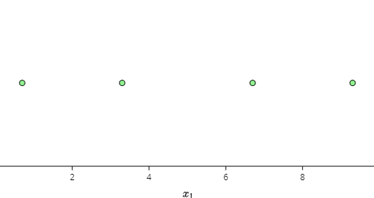
Figure 1. represents a 1D basis plot for a uniform distribution with order 3, with a cardinality of 4.
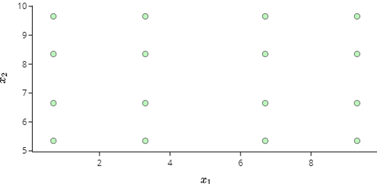
Figure 2. represents a 2D basis plot for 2 uniform distribution with order 3, with a total cardinality of 16.
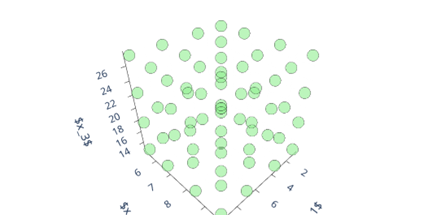
Figure 3. represents a 3D basis plot for 2 uniform distribution and a gaussian distribution with order 3, with a total cardinality of 64.
New plots are added in the Compute Polynomial Application. These include Sobol plots and Polyfit plots. The Sobol plots consist of a maximum of 3 plots mapping to Sobol indices of orders 1,2 and 3.
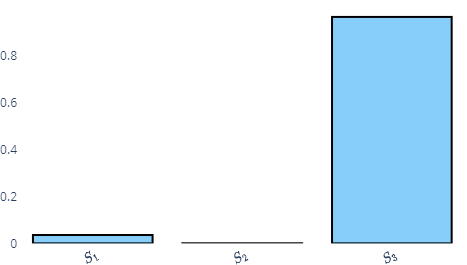
Figure 4. represents a first order sobol plot for 2 uniform distributions and a gaussian distribution, with the input function tan(x1)+log(x2)+x3
The Polyfit plot offers 2 different kinds of plots available for 1D Polynomial and 2D polynomial.
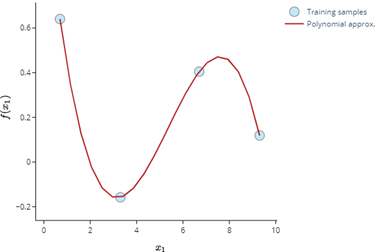
Figure 5. represents a Polyfit plot for 1D polynomial with cardinality 4 and input expression Sin(x).
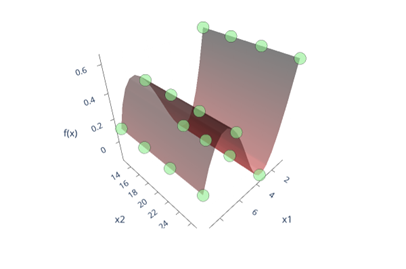
Figure 6. represents a Polyfit plot for 2D polynomial with cardinality 16 and input expression Sin(x).
ERROR-HANDLING
It is important to consider various corner cases to improve a web application. As our workflow is strict, numerous error handling cases needs to be added. The updated app covers various corner cases such as incorrect input function, empty input boxes, missing few steps of the workflow. For example, a user, after creating parameters can jump directly to compute uncertainty and create a polynomial, missing an important step of selecting the basis function. This is handled using Dash input box properties and disabling the input box till the user sets the basis.
DEPLOYMENT OF THE APP
With the main functionalities of the app working, we decided to deploy the app on a server. This was done using Heroku. Heroku is a cloud platform that helps companies to build, deliver and monitor their app.
WHAT’S NEXT?
Minimal changes and updates would be made to the analytical model. Our main aim would be to get a working Offline Model ready within the next 2 weeks, the offline model being really similar to the analytical model, would have a professional use.