" If it could only be like this always – always summer, the fruit always ripe…" —Evelyn Waugh
Hello everyone, this is the final blog in the series of blogs I have written during the coding period of GSoC 2021. These 10 weeks have been a great journey, where I gained a lot of new skills and applied it in the application. This wouldn’t have been possible without the help from my mentors Ashley Scillitoe and Bryn Ubald who guided me throughout the coding period be it with code or theory (even git). Also, a huge thanks to Equadratures community for giving me this opportunity.
Moving on to the dashboard,
The source code for the final application can be viewed here (EQ-uq). The commits, in accordance to the timeline can be viewed in this spreadsheet (Here, I’ve mentioned the important commits I made during the coding period, to view the full commit history, you could visit EQ-uq commits history). There is also a major PR to be made to Equadratures which is currently under work but is being used in the application and is present in my forked repository(Link)
In the first blog, I mentioned the main aim of the web application is to aid the users without any prior knowledge of coding language to perform Uncertainty Quantification using Equadratures. This included creation of two types of models: Analytical and Offline, which I have delineated upon in my previous blogs. Both of these models are quite similar in workflow but have different applications.
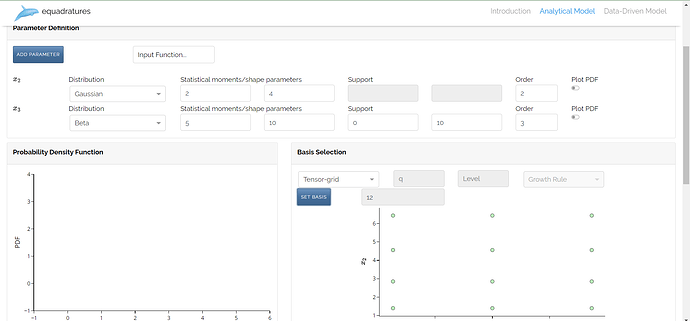
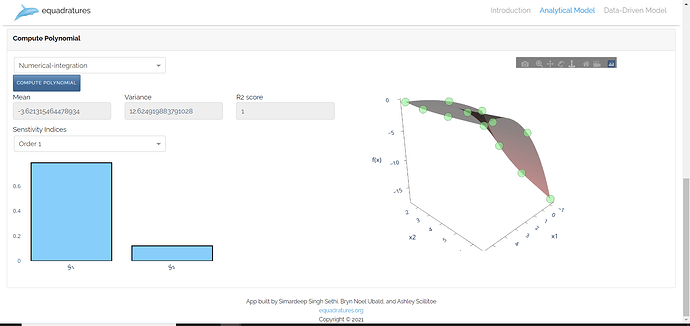
- In the Analytical model we aim to approximate a physical model with uncertain inputs using a polynomial and then we can use that polynomial to compute statistical moments of the output, and to compute sensitivity indices, at a much lower cost than Monte Carlo type methods in the analytical model workflow, the user prescribes an analytical model, and this is evaluated under-the-hood by the app.
- The Offline model is for professional-use, it requires a basic understanding of Polynomial Chaos Expansion and it can be used while running simulations, users can download the DOE or the design of experiment, run their simulations at these points and then upload their model evaluations to understand the Model.
We also had an additional goal of creating another model which would be more data centric and with the main models completed before the timeline, we started working on our stretch goal of creating the data-driven model. This model is a data-centric model where the user can upload custom datasets or use basic datasets such as “Probes” or “Airfoil Noise”.
The deployed application can be viewed at Link.
The Final Product:
Introduction:
The introduction page consists of the motivation for using Equadratures for uncertainty quantification and dwells upon few of many theoretical aspects used in the library, it also introduces the users to the workflow and models that are present in the application.
Analytical Model:
The Analytical and Offline model being quite similar are present on the same page. Few minor changes have been made in the implementation of these models to decrease the time complexity of certain functions on Heroku server.
Following are few images of the models in work:
Parameter Definition:
Set Model:
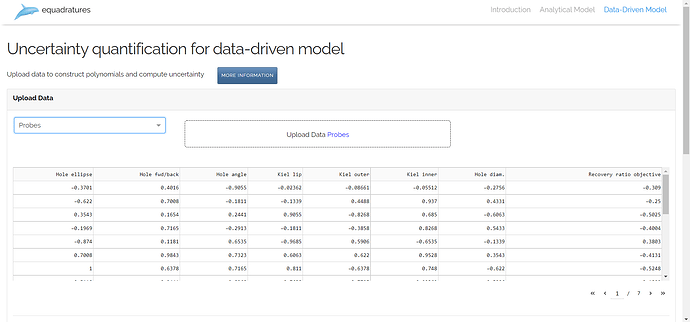
Data Driven Model:
The latest addition to this application is the data-driven model. Unlike analytical and offline model, the user doesn’t need to create parameters manually and can simply upload their data and choose their output variable. This model provides two different methods for distribution selection:
- Canonical Approach
- KDE Approach
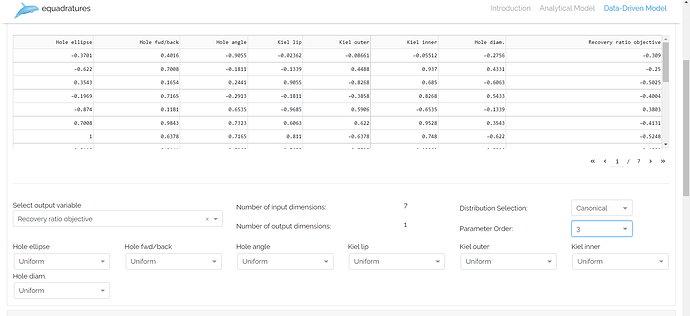
In the canonical approach the users have to manually select the distribution of the input parameters. This method makes use of Scipy fit method to compute the statistical moments, which are then fed to the Equadratures parameter.
In the KDE approach, as the name suggests Kernel Density Estimation is used to create parameters. Here, we use a gaussian kernel to fit a distribution to the data and produce accurate results. The downfall of this approach is that it is computationally expensive and takes much longer time to compute.
Upload Dataset Functionality:
Canonical Approach:
WHAT NEXT?
With the GSoC coding period over and the application being ready to use, there are few modifications that could enhance the user interface and boost the application to be powerful in computation considering both time and space constraints. Features such as KDE implementation in data-driven model takes up a lot of time to create parameters which restricts its use on Heroku, which has a 30 second time-limit. Other enhancements could include new plotting methods in the case of PolyfitPlot with higher dimensions.
So, it’s the end of Google Summer of Code 2021 but not for Open Source, I would love to continue to contribute to Equadratures, add many more features and remove bugs (even those which I create). In the end, it was a great summer filled with opportunities, life lessons and exciting work and as the great Tony Stark quoted:
“Part of the Journey is the End”